Fermion Propagators: Stability of Self-Energy
Table of Links
- Prologue
- Diagrammatic(s) Rules
- Straight-forward Eikonal
- Legacy Bosonization
- Wonton Holography
- Holographic Propagators
- Strange Cuprates
- Stranger Things
- Epilogue
Diagrammatic(s) Rules
In many of the diverse reincarnations of the problem of finite density fermions with the interactions mediated by gapless bosonic excitations the propagator of the latter conforms to the general expression
\ 
\ Among the practically important examples of this ’Mother of all NFLs’ are such seemingly disjoint topics as electromagnetic (i.e., Abelian gauge field) skin effect in metals [1] and quark-gluon (non-Abelian) plasmas [2], spin [3] and charge [4] fluctuations in itinerant ferromagnets and Ising quantum nematics, as well as compressible Quantum Hall effect with screened repulsive interactions [5], in all of which situations ξ = 1 and ρ = 2. By contrast, normal skin effect and antiferromagnetic fluctuations in doped Mott insulators are described by ξ = 0, ρ = 2, while compressible Quantum Hall Effect with the unscreened Coulomb interactions corresponds to ξ = 1, ρ = 1.
\ Over several decades much effort has been made towards ascertaining the effects of the interaction (1) on the FL propagator with a finite chemical potential µ
\ 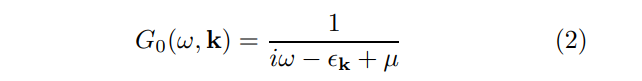
\ whose Fourier transform in the spacetime domain reads
\ 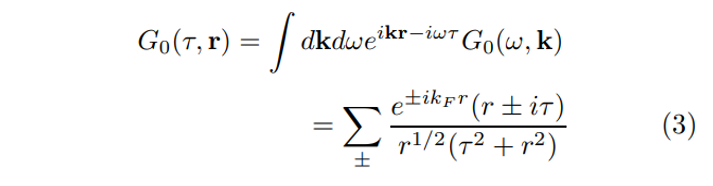
\ Previous diagrammatic approaches to this problem sought out to investigate the stability of the first-order self-energy
\ 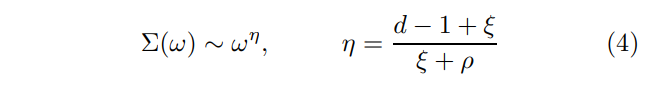
\ against higher-order corrections. For a choice of parameters conspiring to yield η = 1 the self-energy (4) acquires an extra factor ln ω.
\ In the early analyses it was argued that the self-energy retains its functional form (4) to all orders in perturbation theory for any finite N, provided that the FS curvature is properly accounted for [6–8]. This conclusion was drawn on the basis of self-consistent Eliashberg-type diagrammatics which, in turn, relies on the generalized Migdal theorem to control vertex corrections.
\ Utilizing the conjectured all-orders result (4) one arrives at the expression
\ 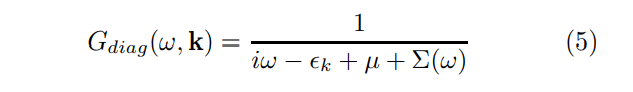
\ where the self-energy is a power-law function of energy with only a weak momentum dependence. To account for a FS curvature κ the fermion dispersion can be expanded in the vicinity of the (Luttinger) FS traced by the unit normal n
\ 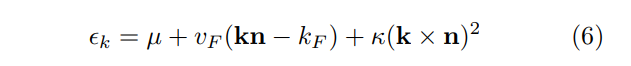
\ Upon Fourier transforming (5) one finds that at the largest spatial separations the equal-time propagator demonstrates a power-law behavior
\ 
\ Moreover, in the complementary limit of large temporal separations the leading term in the all-orders ’nearfield’ propagator retains its non-interacting form [7]
\ 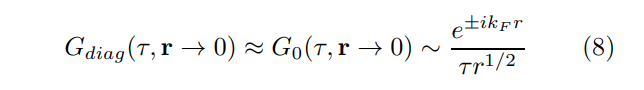
\ although the sub-leading corrections bear some nontrivial τ-dependence (see next sections).
\ It has also noted that the algebraic behaviors (7,8) hold due to the presence of a pole in the integration over ǫk in (5) while in its absence a different functional behavior sets in. However, the latter was predicted to occur only in the (arguably, unphysical) limit N → 0.
\ Contrary to the earlier expectations, though, the refined analyses of higher-order corrections to (4) found them to be singular, albeit suppressed by extra powers of 1/N [9]. A number of attempts to get an analytic handle on the higher-order effects has been made [10] but their full bearing on the problem of interest remains unclear.
\ Furthermore, a naive generalization of the above calculations to finite temperatures appears to be problematic as (4) picks up a singular contribution Σ(0) [4]. This problem is particularly severe in those situations where gauge invariance prevents the mediating transverse gauge field A⊥ = A × k/k from developing a thermal mass (no magnetostatic screening in normal metals).
\ 
\ A simpler - yet, questionable - practical recipe for dealing with this harmonic would be to ignore it altogether - as an artifact of the gauge-non-invariant nature of the fermion propagator- or, more formally, have it absorbed into the renormalized chemical potential.
\ 
\
:::info Author:
(1) D. V. Khveshchenko, Department of Physics and Astronomy, University of North Carolina, Chapel Hill, NC 27599.
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
You May Also Like

Ethereum Set to Debut ‘Key to Layer-2 Scaling’ as Fusaka Upgrade Clears Final Test

IBM’s Quantum ‘Cat’ Roars: 120-Qubit Breakthrough Pushes Bitcoin’s Encryption Risk Closer
